NPTEL An Introduction to Artificial Intelligence Week 8 Assignment 8 Solutions Jan-Apr 2024 quiz 8

Draft version... keep watching the description for updates


Update : Q 4. Ans 0.45

All of you cross check my answers and let me know your views .

@bhagyalakshmi5543:
Question 1: P(cavity | ¬ toothache) + P(cavity | catch).
= 0.072 +0.008 + 0.108+0.072
=0.26 (rounded off)
Question 4 : Solved it as follows... By bayees theorem
p(A(T)/X(T)B(F) = ( p (X(T)B(F)/p(A(t)) X p(A(t) )
----------------------------------------------
(P(X(T)B(F))

numerator = p (X(T)/p(A(t)) x B(F)/p(A(t) X p(A(t) ( Given A X and B are independent)
0.3 X 0.5 X 0.5 = 0.06
Denominator = 0.4 (0.3 X 0.5 ) + 0.6(0.2 X 0.6) = 0.132

Therefore answer = 0.06/0.132 = 0.45 (rounded to 2 digits)

Thanks to @Vanshikajain8087 for partial input to solve this problem....




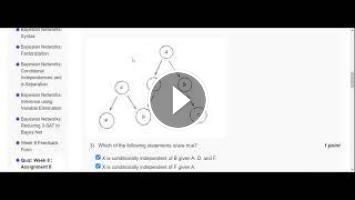
Question 5: A F -1 each (independent) = 2
X B E C - 2 combinations each (one parent) =8
D - 4 combinations (two parents) =4
-----------------------------------
Total 14


@user-cm8ms2xe5y
I think 9 , 10 you can solve it by variable elimination method... I solved it differently (using joint distribution) as follows
Q 9) P (MC | E , ¬ B) = ?
You need to sum over .....Alarm because i t is hidden (you need to consider all combinations)
e ¬b = 0.29 (0.71) from joint distribution

Therefore P(MC) = p(A) * p(MC) + (p(¬ A) * p (MC)
= 0.29 * 0.7 + 0.71 * 0.01
=0.203 + 0.0071 = 0.2101
Q 10)....Similar logic as above

@tarunikachaudhari12
You need to consider all possible combinations given earth quake
0.95 * 0.7 + 0.05 * 0.01 (earth quake +burglergy +Alarm mary cal + E B no alarm Mary call)
+0.29 * 0.7 + 0.71 * 0.01 (earth quake +no burglergy +Alarm mary cal + E ¬b no alarm Mary call))
=0.8756

@tarunikachaudhari12

Q2 . What is the probability that you chose the unfair coin?
There are 1000 coins and the probability that a unfair coin is chosen in 1/1000 ( the probability that it will show up heads 10 times is 1 (it has heads both sides) and hence it will not be considered ) there fore m +n = 1000 + 1 =1001


All based on my thinking only ..
Some one please cross check......

No more updates . I am tired .. need to rest now...
let us wait for the results

Analysis after the results
You should have got 70... A bit disappointed . Thanks to Thanks to @vishalsai6903 and @Vanshikajain8087

2nd question... It was my mistake. The answer should be probability of all 10 heads turning up when unfair coin turns up / (all 10 heads turning up when unfair coin turns up + all 10 heads turning up when fair coin turns up)
Numerator.. = 1/999
Denominator = (999/1000) X 1/ 2^10 (probability of fair coin turning and all heads up + (1/999) X1

which turns out to be 1024/2023 = hence answer is 1024 + 2023 = 3047.... lost 10 marks because I could not look it yesterday.. Not convinced with question 1 and question 10...will check with TAs

Q 10 .. Unbelievable that the probability can be so low . some thing is wrong some where.
Q 1 .. did not understand where I went wrong

Please let me know what others think